作者Charlesna 摘要解题思路 求二分图的最大匹配,用匈牙利算法。 根据 i j 的和为奇数或者偶数,把所有点分成两个集合。任何一个奇数和的四周最多有四个和为偶数的点,但是因为有些点不能够进行匹配,所以需要用到二分图匹配进行选择。 代码匈牙利算法用于求解无权二分图(unweighted bipartite graph)的最大匹配(maximum matching)问题861 二分图的最大匹配 时间复杂度 没有任何一个点在多条边上,称为一个匹配。 虽然是无向图,但是存边存的是有向边,算法是只看左边的情况。所以只需要存左边指向右边就可以了。

二分图 Oi Wiki
二分图最大权匹配
二分图最大权匹配-目录学习篇二分图以及其最大匹配匈牙利算法二分图最大匹配变形题最小顶点覆盖 最大独立集DAG图的最小路径覆盖水题集hdu 63:男女最大匹配hdu 1150:机器最少重启次数hdu 1151:DAG最小覆盖路1068:最大没有联系的男女个数hdu 1281 :骑士最大放置数学习篇二分图以及其最大匹配一、什么是二分图二分图最大匹配: 给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)。 首先我们先了解两个概念
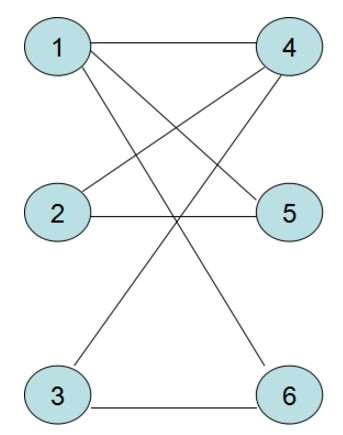


Bipartite Graph 二分图 Elmagnifico S Blog
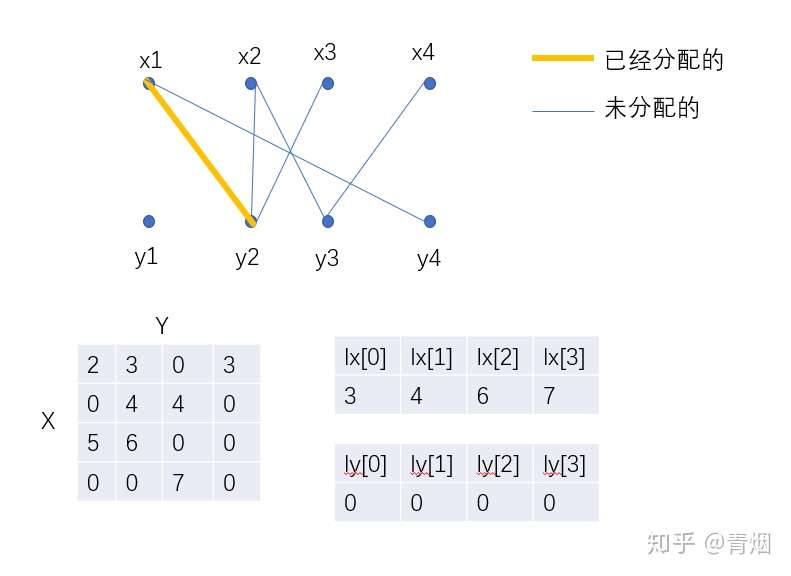
的权值.左侧带权凸二分图上的最大权值匹配问题 对应着一类经典的调度问题2:给定任务集合和时 间片集合,其中每个任务有释放时间、期限和权值, 且执行时间为单位时间,其调度目标是寻找最大权 值的可行调度任务子集.凸二分图动态匹配问题在求二分图最大权匹配的km算法 1951 这个算法的本质还是不断的找增广路;KM算法是通过给每个顶点一个标号(叫做顶标)来把求最大权匹配的问题转化为求完备匹配的问的。 设顶点Xi的顶标为Ai,顶点Yi的顶标为Bi,顶点Xi与Yj之间的边权为wi,j。在算法执行过程中的任一时刻,对于任一条边POJ 2400 Supervisor, Supervisee (二分图最大权匹配) @ 千千 / 发表于 17 年 04 月 30 日 / 二分图 / 956 次围观 Description Suppose some supervisors each get to hire a new person for their department There are N people to be placed in these N departments Each supervisor interviews all N people, and ranks them according
OI Wiki 二分图最大权匹配 键入以开始搜索 OIwiki/OIwiki 简介 语言基础 算法基础 搜索 动态规划 字符串 数学 数据结构 图论 计算几何 杂项 专题 关于 Hulu school OI Wiki OIwiki/OIwiki 简介 简介算法导论——二分图最大匹配 二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。Server time 2107
模板二分图最大权完美匹配km算法的更多相关文章 二分图最大权完美匹配km算法 km算法二分图 km求得二分图与普通二分图的不同之处在于此二分图的每条边(男生女生)上都附了权值(好感度)然后,求怎样完美匹配使得权值之和最大 这,不止一般的麻烦啊作者wangdh15 摘要解题思路 二分图匹配,横纵坐标和为奇数的点为一个集合,横纵坐标和为偶数的点为一个集合。 然后求这个二分图的最大匹配即可。 个人博客 代码1、二分图、最大匹配 什么是二分图:二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。


蒟蒻图论 二分图最大带权匹配 蒟蒻のblog
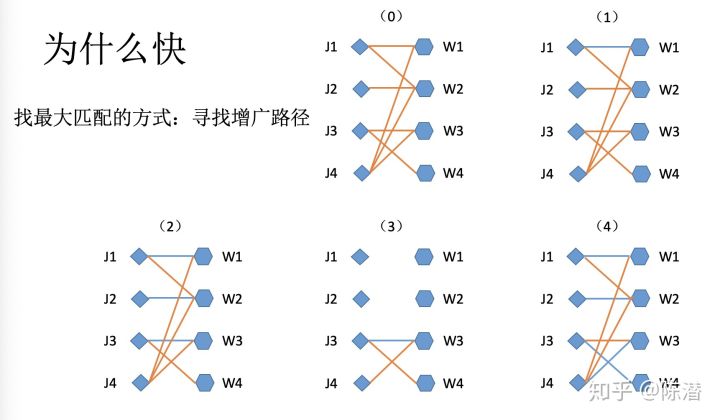


匈牙利算法 默默的点滴
Universal Online Judge 鄂公网安备 号;作者wangdh15 摘要解题思路 二分图匹配,横纵坐标和为奇数的点为一个集合,横纵坐标和为偶数的点为一个集合。 然后求这个二分图的最大匹配即可。 个人博客 代码目录学习篇二分图以及其最大匹配匈牙利算法二分图最大匹配变形题最小顶点覆盖 最大独立集DAG图的最小路径覆盖水题集hdu 63:男女最大匹配hdu 1150:机器最少重启次数hdu 1151:DAG最小覆盖路1068:最大没有联系的男女个数hdu 1281 :骑士最大放置数学习篇二分图以及其最大匹配一、什么是二分图
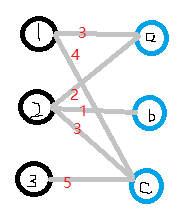


图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客



0x68 图论 二分图的匹配 码农家园
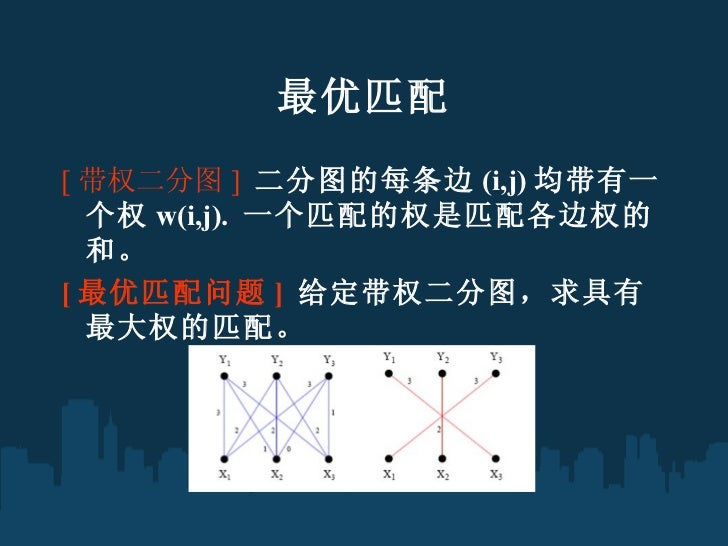
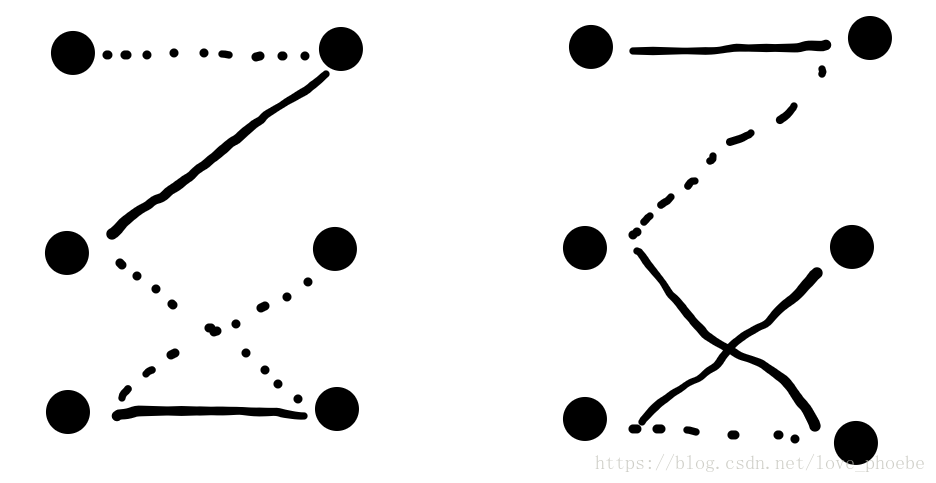
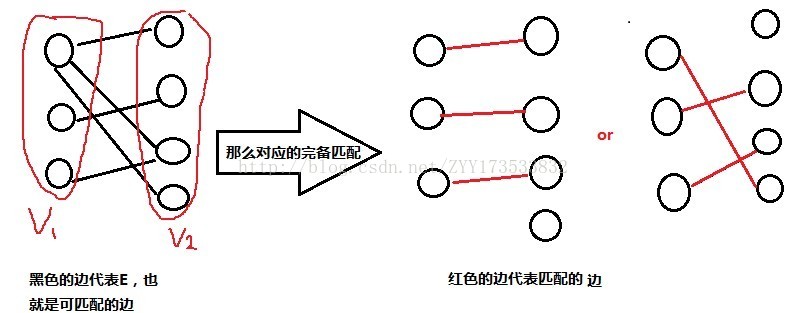
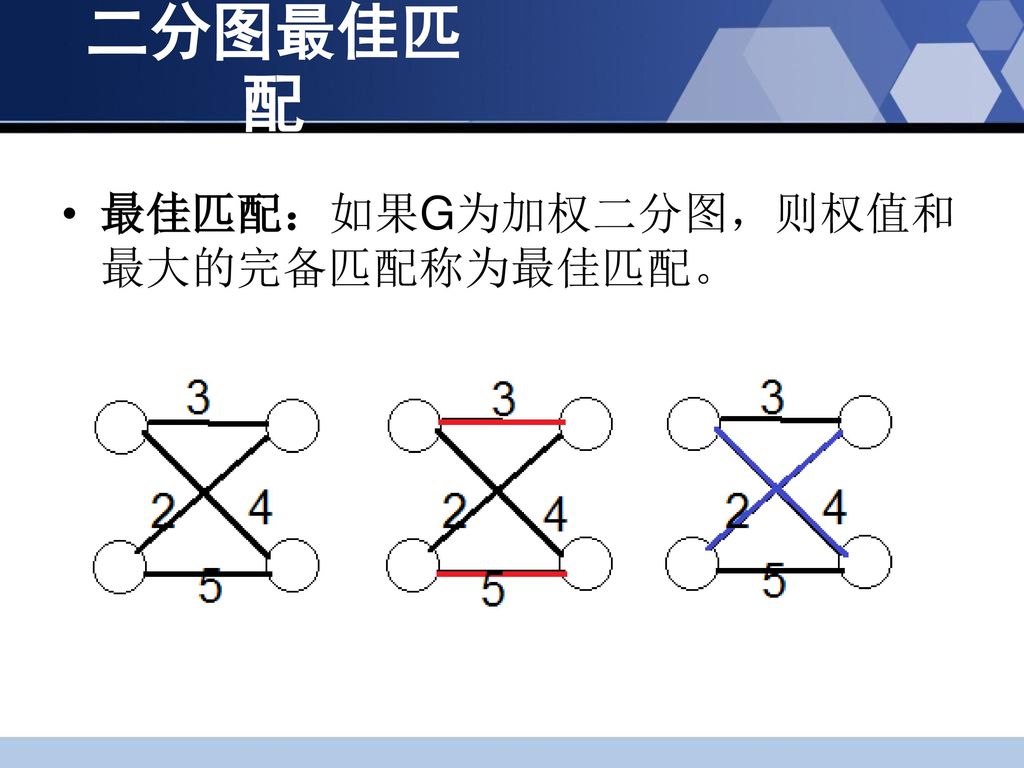
完美匹配一定是最大匹配, 但并非每个图都存在完美匹配 最优匹配(带权最大匹配) 在带有权值边的图中,匹配边上的权值和最大的匹配 二分图中, 一般x和y集合顶点个数相同, 最优匹配也是一个完备匹配 如果个数不相等, 可以通过补点加0边来转化二分图的最优匹配( 算法) 二分图的最优匹配(KM 算法) KM 算法用来解决最大权匹配问题: 在一个二分图内,左顶点为 X,右顶点为 Y,现对于每组左右连 接 XiYj 有权 wij,求一种匹配使得所有 wij 的和最大。在二分图的匹配当中,有两种常见的匹配目标,一个是最大匹配,即尽可能多地将 中的点配对;另一个是最佳匹配,最佳匹配的应用场景则是在带权二分图中,最佳匹配就是 中所有的点都与 中的某一个点匹配成对,并且能够使得这些边的权值之和最大的匹配。 显然,满足最大匹配的子图可能不唯一,而满足最佳匹配的子图,由于不同边可能有一样的权值,也可能不唯一。



二分图 Oi Wiki



二分图最大匹配 第1页 一起扣扣网
Acm二分图的最大权匹配 题目 给出一个二分图 每条边都有自己的边权 让你选择一些边 仍旧满足"任意两边的端点不重合" 问最大的边权和是多少 如何解决这个问题? 使用km算法 km算法是二分图最大权匹配km算法 二分图最大权匹配km算法 分类: C 算法 2316 102人阅读 评论(0) 收藏 举报 百度百科是错的,关于相等子图的那一块。 穷举的效率-n!Acm二分图的最大权匹配 题目 给出一个二分图 每条边都有自己的边权 让你选择一些边 仍旧满足"任意两边的端点不重合" 问最大的边权和是多少 如何解决这个问题? 使用km算法 km算法是



图论2 江川 Ppt Download



二分图学习记之km算法二分图最大权完美匹配 寒冰大大 博客园
给定一张二分图,左右部均有 $n$ 个点,共有 $m$ 条带权边,且保证有完美匹配。 求一种完美匹配的方案,使得最终匹配边的算法导论——二分图最大匹配 二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。时间内求出二分图的 最大权完美匹配。 考虑到二分图中两个集合中的点并不总是相同,为了能应用 km 算法解决二分图的最大权匹配,需要先作如下处理:将两个集合中点数比较少的补点,使得两边点数相同,再将不存在的边权重设为



二分图 网络流初步 Jzp 的博客 洛谷博客



图 二分图最大权匹配 Visayafan 博客园
从前一个和谐的班级,有 $n_l$ 个是男生,有 $n_r$ 个是女生。编号分别为 $1, \dots, n_l$ 和 $1, \dots, n_r$。 有若干个这样的条件模板二分图最大匹配 ZJOI07 矩阵游戏 ZJOI09假期的宿舍 飞行员配对方案问题 最小路径覆盖问题 USACO05JANMuddy Fields G 国家集训队部落战争 TJOI13攻击装置 HEOI16/TJOI16游戏 TJOI14匹配 长脖子鹿放置 骑士共存问题 模板二分图最大权完美匹配 Air Raid时间内求出二分图的 最大权完美匹配。 考虑到二分图中两个集合中的点并不总是相同,为了能应用 km 算法解决二分图的最大权匹配,需要先作如下处理:将两个集合中点数比较少的补点,使得两边点数相同,再将不存在的边权重设为



求一部1 H8 X P Www Dingjisc Com


二分图带权匹配 推箱子问题的思考
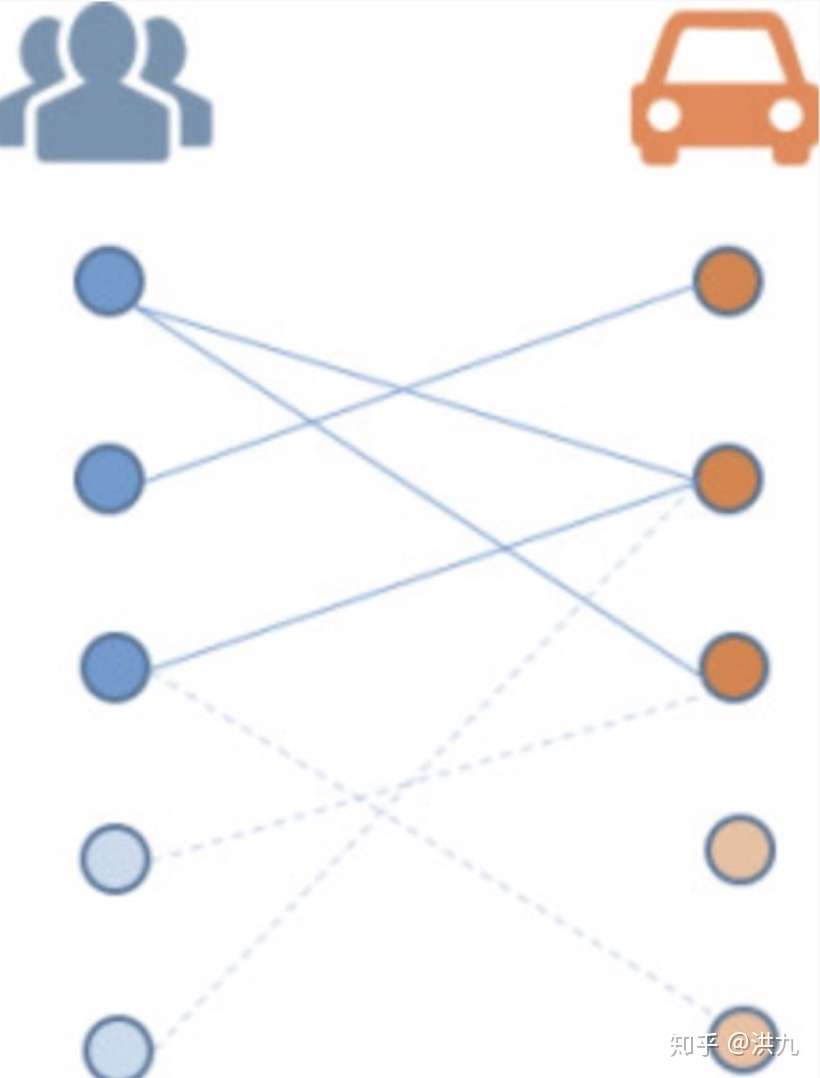
POJ 2400 Supervisor, Supervisee (二分图最大权匹配) @ 千千 / 发表于 17 年 04 月 30 日 / 二分图 / 956 次围观 Description Suppose some supervisors each get to hire a new person for their department There are N people to be placed in these N departments Each supervisor interviews all N people, and ranks them accordingKM算法的正确性基于以下定理: 若由二分图中所有满足AiBi=wij的边C(i,j)构成的子图(即相等子图)有完备匹配,那么这个完备匹配就是二分图的最大权匹配 基本概念 1完备匹配 设G=<V1,V2,E>为二分图,V1<=V2,M为G中的一个最大匹配,且M=V1,则称M为V1到V2的完备匹配。二部图最大权匹配_学习记录 二分图匹配问题与匈牙利算法及KM算法 一、前言在论文"Realtime Event Detection on Social Data Streams"中,作者首先在每一个时间窗口(分钟级)内利用社区发现算法(Louvain method)得到一个聚类,然后采用带权二分图最大匹配(maximum weighted


Km算法详解 模板 二分图最大权值匹配 Shyoldman的博客 Csdn博客
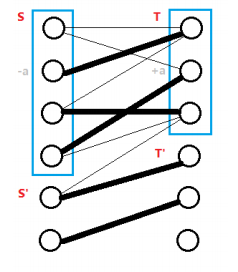


二分图最大权匹配 Oi Wiki



二分图最优匹配 Km算法 简书



0x68 图论 二分图的匹配 码农家园
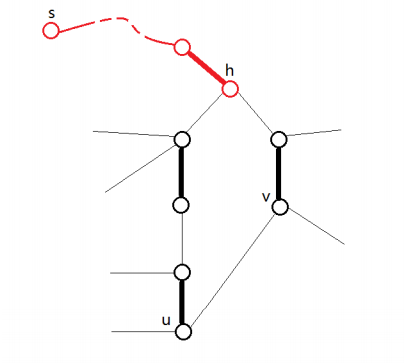


一般图最大匹配 Oi Wiki


算法竞赛入门经典 训练指南



Python实现km算法
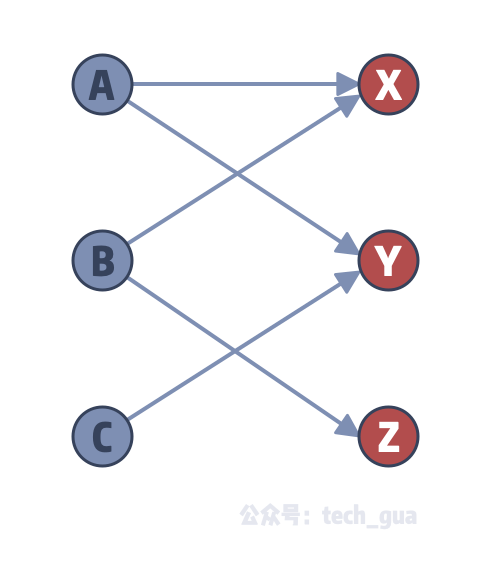


二分匹配的最大流思维 一瓜算法小册



二分图匹配 最大匹配 匈牙利算法 完美匹配 最大权值匹配 Km算法 Weekness的博客 Csdn博客


二分图最大权值匹配算法 Km算法 和匈牙利算法 知乎
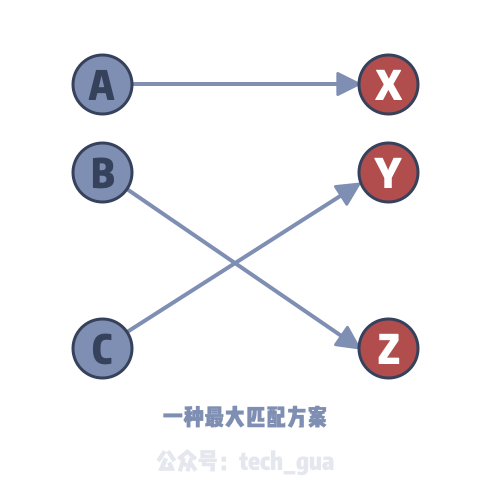


二分匹配的最大流思维 一瓜算法小册



Uoj 80 二分图最大权匹配 Konjak魔芋 博客园


算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog



0x68 图论 二分图的匹配 码农家园


Acm图论


二分匹配的最大流思维 一瓜算法小册



Acm图论


匈牙利匹配 匈牙利法解指派问题 匈牙利最优匹配法 二分图最大匹配算法


二分图最大权值匹配算法 Km算法 和匈牙利算法 知乎



模板 二分图最大权完美匹配km算法


二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 傻子是小傲娇的博客 大钊 Csdn博客
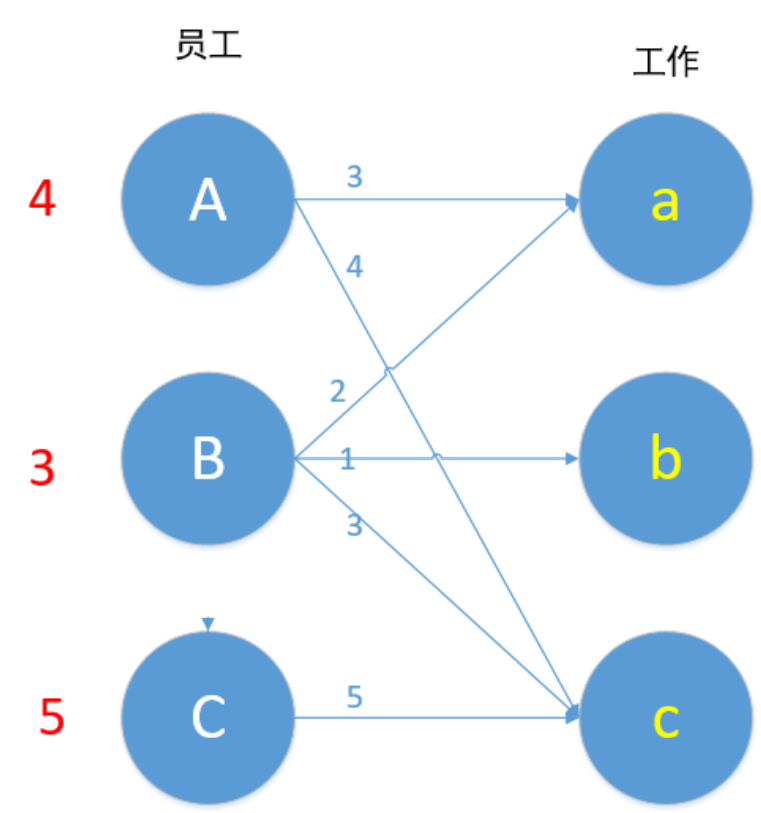


二分图最大权匹配问题 Km算法讲解 Hdu 2255 奔小康赚大钱 Kongbursi 博客园


算法竞赛入门经典 训练指南


二分图匹配 匈牙利算法和km算法简介 Ppt 十八文库



图论2 江川 Ppt Download



Bipartite Graph 二分图 Elmagnifico S Blog
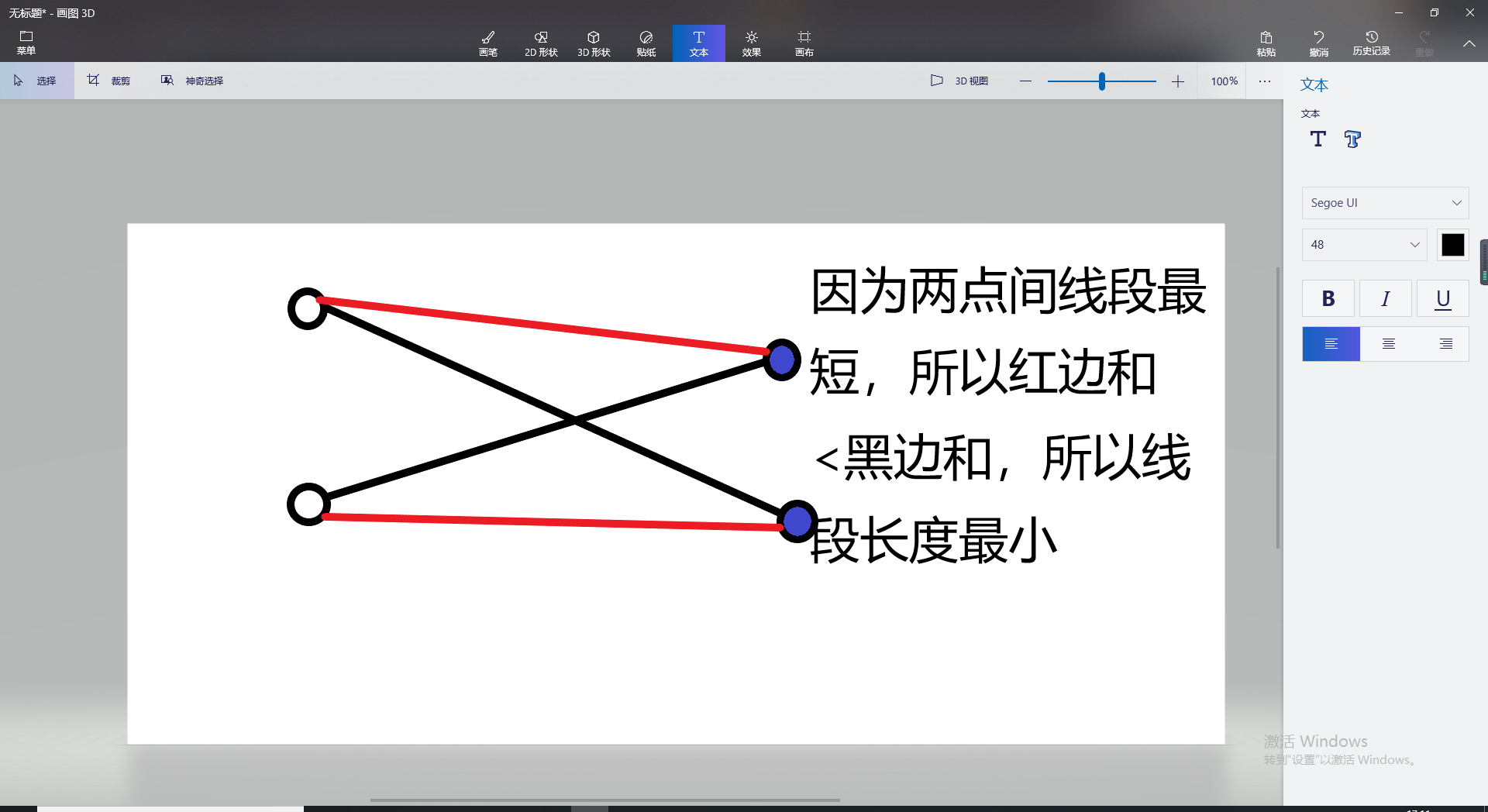


Acwing 375 蚂蚁 Acwing
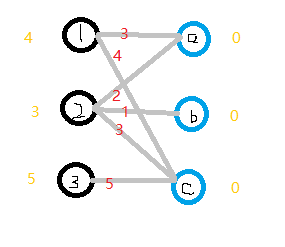


图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客
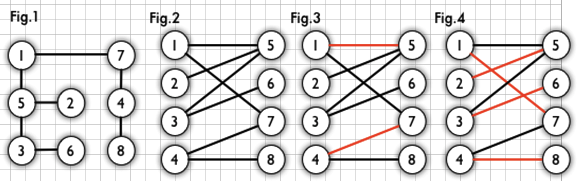


匈牙利算法 Km算法详解及java实现 刘航的oschina博客 Oschina
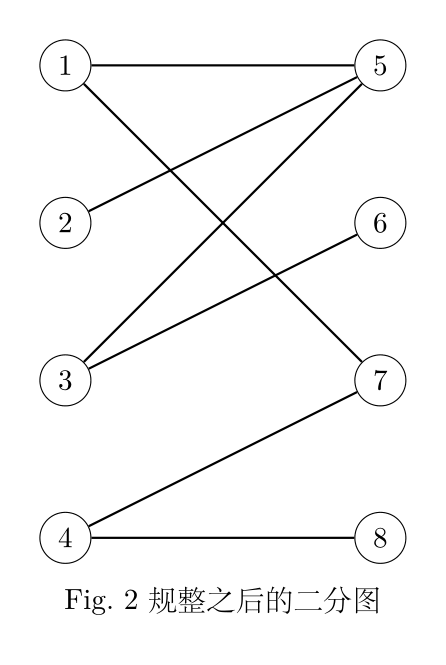


二分图最大匹配问题与匈牙利算法的核心思想 始终



Python实现km算法
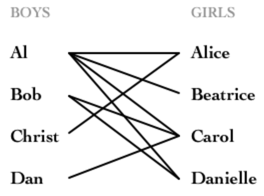


图论在计算广告中的应用 知乎


二分图带权匹配 推箱子问题的思考



Hdu 3395 费用流 二分图的最大权匹配 Hexianhao的博客 Csdn博客


两个步骤 解析滴滴如何为你找到司机的 人人都是产品经理



二分图最优匹配 Km算法 简书
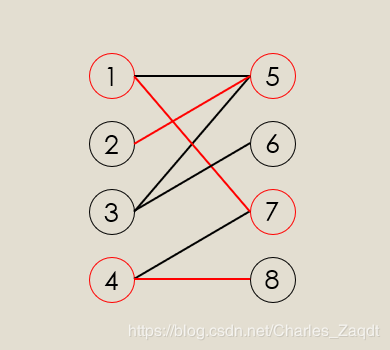


干货 二分图详解 知乎
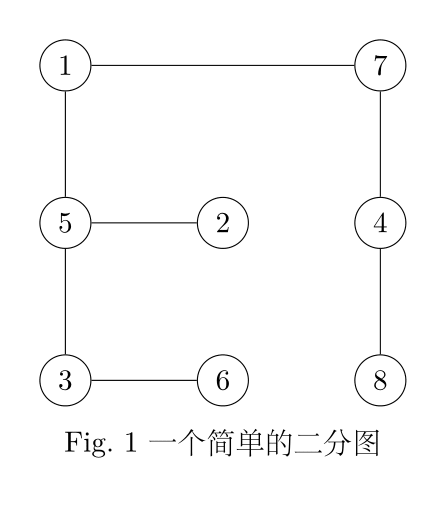


二分图最大匹配问题与匈牙利算法的核心思想 始终



转 带花树 Edmonds S Matching Algorithm 一般图最大匹配


算法导论 二分图最大匹配 简书


二分图最大权匹配km算法 紫芝的博客 Csdn博客 二分图最大权匹配



图匹配 Oi Wiki


图论2 江川 Ppt Download



67 二分图的匹配 图论 特殊图 Coursera


算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog



泽民博客 Jekyll Theme


演算法筆記 Matching


Uvalive 4043 Ants 二分图最大权匹配km算法 H Z Cong 博客园



二分图最大匹配 第1页 一起扣扣网


Sk Rokol7g1mam



分享 二分图最大匹配 Poj3041 1024toyou Com
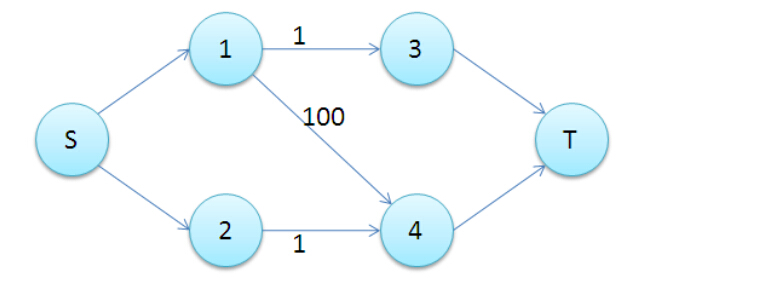


二分图带权匹配费用流模型建立 Song Csdn博客



二分图最大权完美匹配 Km算法 Khasehemwy的博客 Csdn博客


最大二分图匹配 零一人生


二分图匹配 图文 百度文库
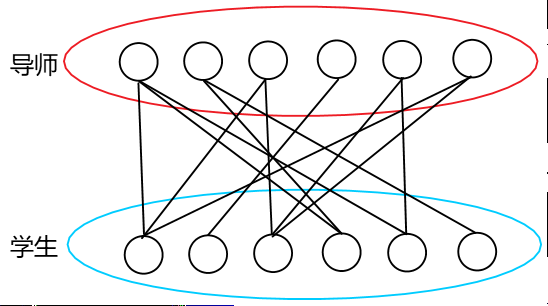


二分图带权最大匹配费用流 简单理解二分图与匈牙利算法 Weixin 的博客 Csdn博客



图论2 江川 Ppt Download


Poj 2195 Going Home 二分图完美匹配 极限定律 C 博客
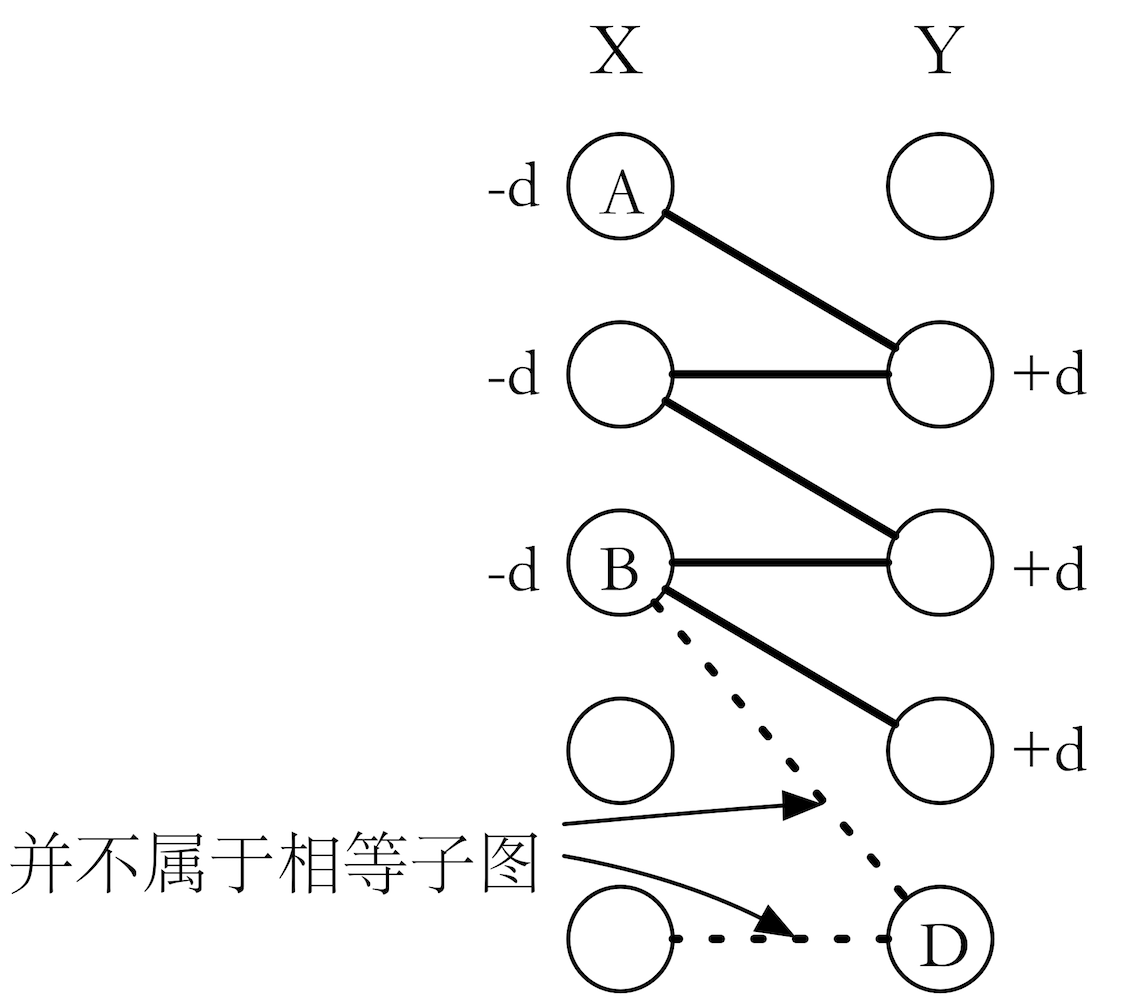


Kuhn Munkres 算法详细解析 Sengxian S Blog
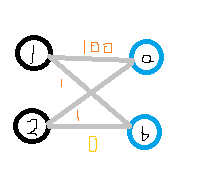


图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客



分享 二分图最大匹配 Poj3041 1024toyou Com



二分图匹配 匈牙利算法 程序员大本营
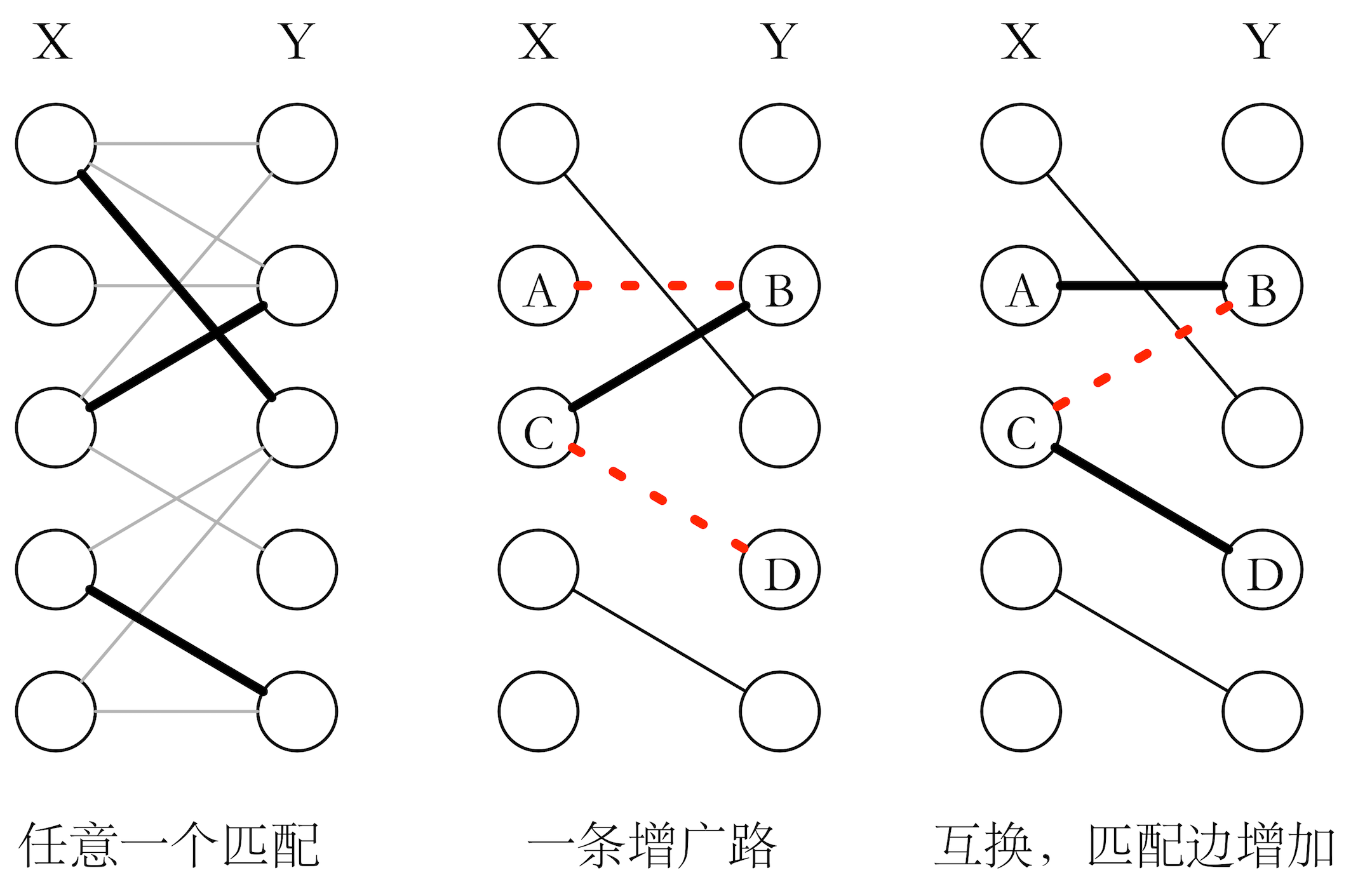


Kuhn Munkres 算法详细解析 Sengxian S Blog
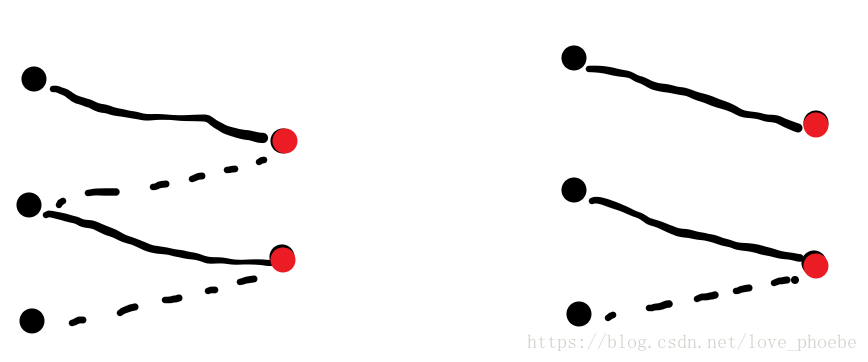


二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 Osc 779ncf3o的个人空间 Oschina
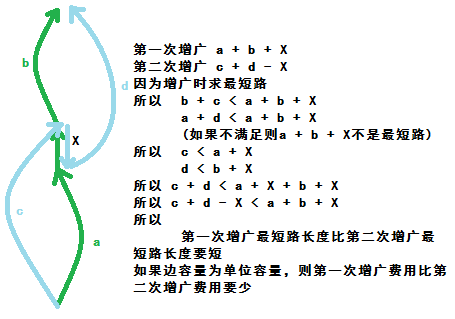


费用流做二分图最大权匹配 我数学不好 Csdn博客



二分图最大匹配 第1页 一起扣扣网
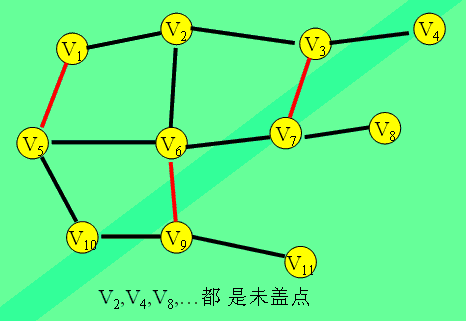


匈牙利算法



二分图最大匹配 第1页 一起扣扣网



图 二分图最大权匹配 Visayafan 博客园



二分图带权匹配km算法与费用流模型建立



最小费用最大流 Bn S Blog


Poj 2195 Going Home 二分图完美匹配 极限定律 C 博客



无权二分图的最大匹配求解 匈牙利算法求解 程序员大本营



Hdu 34 二分图最大权匹配 牛客博客



Hdu 34 二分图最大权匹配 牛客博客



Km算法原理 证明 鱼 渔 博客园



二分图学习记之km算法二分图最大权完美匹配 寒冰大大 博客园
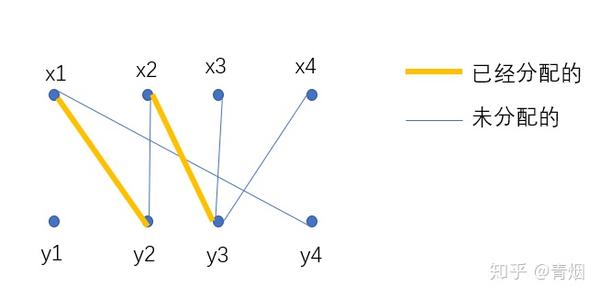


Le5lrblimez Rm
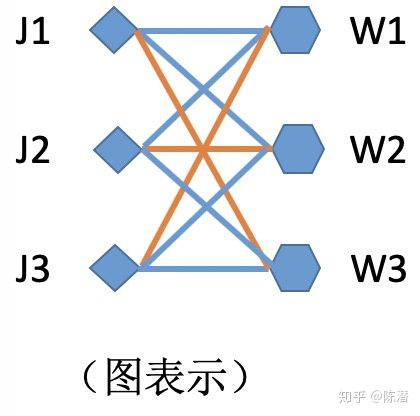


匈牙利算法 默默的点滴



匈牙利算法 Kuhn Munkres 算法 Osc 8vgjpfw9的个人空间 Oschina


Bipartite Matching And Hungarian Algorithm Sen Yang


二分图带权匹配 推箱子问题的思考



P6577 模板 二分图最大权完美匹配 牛客博客



二分图最大匹配 第1页 一起扣扣网
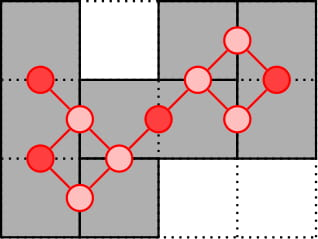


匹配算法 Daltao S Blog


图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客
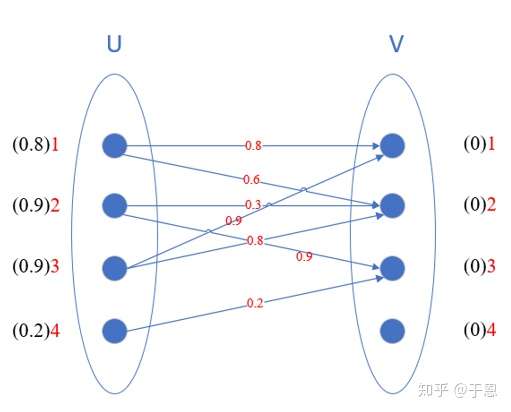


多目标跟踪之数据关联 匈牙利算法 Km算法 知乎


同济大学icpc暑假训练8月16日二分图及其应用 哔哩哔哩 つロ干杯 Bilibili



No comments:
Post a Comment